1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/aJaVmZ1u
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
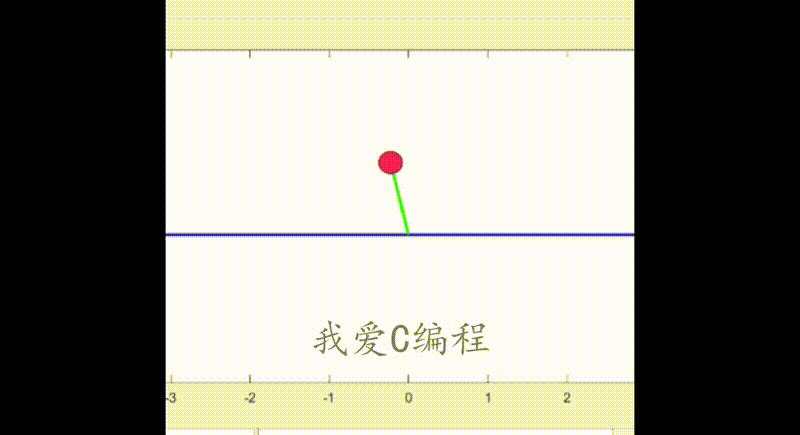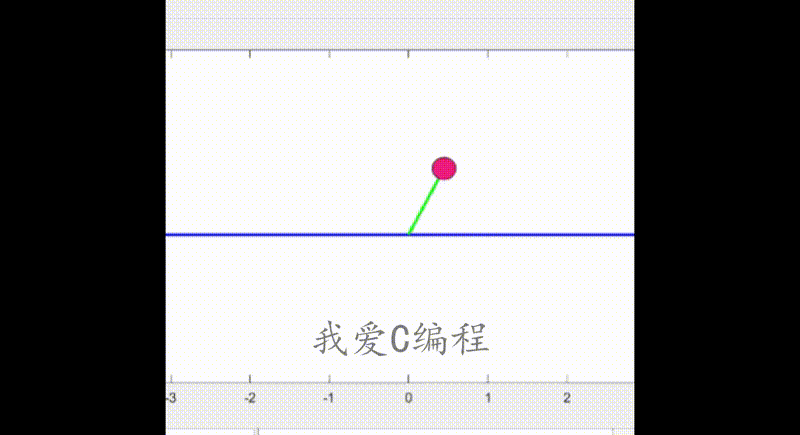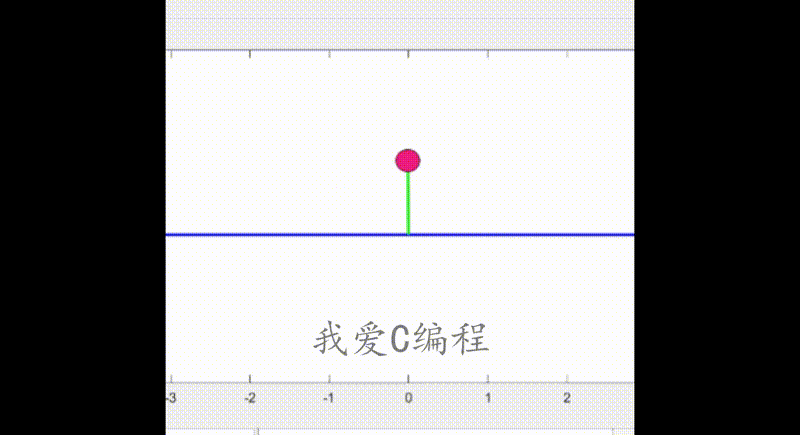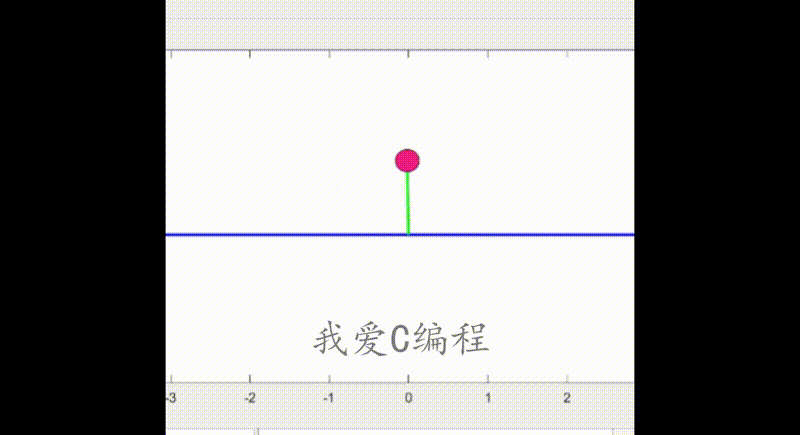
3.算法概述
强化学习是一种使智能体在环境中通过不断试错和学习来优化其行为策略的方法。在钟摆直立平衡控制问题中,我们希望通过强化学习让智能体学会控制钟摆,使其尽可能长时间地保持直立状态。Q-learning 作为强化学习中的经典算法,在解决这类问题中具有重要的应用价值。
Q-Learning是一种无模型的强化学习算法,它能够使代理(Agent)在与环境互动的过程中学习最优策略,无需了解环境的完整动态模型。在迷宫路线规划问题中,Q-Learning被用来指导代理找到从起点到终点的最优路径,通过不断尝试和学习来优化其行为决策。
Q-Learning属于值函数方法,其核心思想是通过迭代更新一个动作价值函数Q(s,a),该函数评估在状态s采取动作a后,预期的长期奖励。更新过程遵循贝尔曼方程,同时利用了探索(Exploration)和利用(Exploitation)的概念,以平衡对未知状态的探索和已知有利路径的利用。
4.部分源码
...............................................................
% Q 学习设置
% 训练的阶段数为50
Mepchs = 50;
Rwds = [];
% 初始化 Q 学习对象 Q_train,传入初始区域数量和状态 - 动作空间的边界
Q_train = func_Q(Nini, Xmin, Xmax);
save Q1.mat Q_train;
tau = 0;
for j=1:Mepchs% 开始训练循环,循环 Mepchs 次,即进行 Mepchs 个训练阶段
j
% 调用 func_Qlearning 函数进行 Q 学习,传入学习标志 1(表示学习)、绘图标志 0(表示不绘图)、Q 学习对象 Q_train
[reward_sum2,Q_train,~] = func_Qlearning(1,0,Q_train);
if j == Mepchs%学习后的模型
save Q2.mat Q_train;
end
Rwds(j) = reward_sum2;
figure;
plot(Rwds,'-r>',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.9,0.0]);
xlabel('训练次数');
ylabel('奖励值');
grid on
%训练前控制效果
figure;
[Rws1,Qtab1,th1] = func_Qlearning(0,1,Q_train);
%训练后控制效果
Qtabn = load('Q2.mat');
After_Training = Qtabn.Q_train;
figure;
[Rws2,Qtab2,th2] = func_Qlearning(0,1,After_Training);
figure;
plot(th1,'b');
hold on
plot(th2,'r','LineWidth',2);
hold on
xlabel('训练次数');
ylabel('倒立摆角度变化');
legend('训练前','训练后');
0Z_017m
---