1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/aJWUmJdu
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
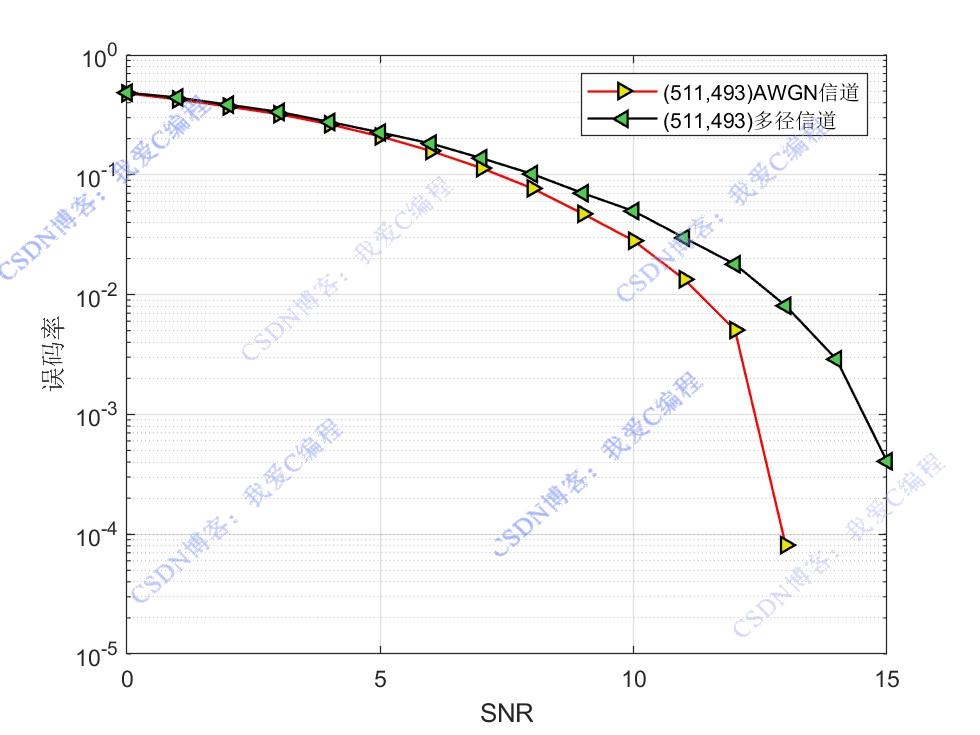
3.算法概述
BCH 码(Bose - Chaudhuri - Hocquenghem Codes)是一类重要的线性分组码,在通信和存储系统中广泛应用。它能够纠正多个随机错误,具备强大的纠错能力。钱搜索译码算法的优势在于其相对简单直观,计算复杂度较低。在硬件实现方面,它可以通过移位寄存器和有限域运算单元高效实现。在通信领域,BCH 码结合钱搜索译码算法常用于卫星通信、数字视频广播等场景,用于纠正信道传输过程中引入的错误,确保数据的可靠传输。在存储系统中,如磁盘存储、闪存存储等,BCH 码及其译码算法可用于纠正存储和读取过程中出现的错误,提高数据存储的可靠性 。
4.部分源码
% 定义一个名为 bchencoder 的函数,用于实现 BCH 编码
% 输入参数:
% data:待编码的数据序列
% genpoly:生成多项式,是一个行向量
% n:编码后码字的长度
% k:原始数据的长度
% 输出参数:
% code:编码后的码字序列
function code=bchencoder(data,genpoly,n,k);
% 初始化一个长度为 n - k 的零向量 bb,用于存储编码过程中的中间结果
bb=zeros(1,n-k);
% 从数据序列的最后一位开始,逐位处理原始数据
for i=k:-1:1
% 计算反馈值,通过将当前数据位与 bb 向量的最后一位进行异或运算得到
feedback = xor(data(i), bb(n-k));
% 判断反馈值是否不为 0
if feedback~=0
% 从 bb 向量的最后一位开始,向前逐位更新 bb 向量
for j=n-k:-1:2
% 判断生成多项式的对应位是否不为 0
if genpoly(n-k-j+2)~=0
% 如果生成多项式的对应位不为 0,则将 bb 向量的前一位与反馈值进行异或运算,更新当前位
bb(j)=xor(bb(j-1),feedback);
else
% 如果生成多项式的对应位为 0,则直接将 bb 向量的前一位赋值给当前位
bb(j)=bb(j-1);
end
end
% 将反馈值赋值给 bb 向量的第一位
bb(1)=feedback;
else
% 如果反馈值为 0,从 bb 向量的最后一位开始,向前逐位更新 bb 向量
for j=n-k:-1:2
% 直接将 bb 向量的前一位赋值给当前位
bb(j)=bb(j-1);
end
% 将反馈值(此时为 0)赋值给 bb 向量的第一位
bb(1)=feedback;
end
end
% 将 bb 向量和原始数据序列拼接在一起,得到最终的编码后的码字序列
code=[bb,data];
14_001m
---