1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/ZJWWmZZr
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
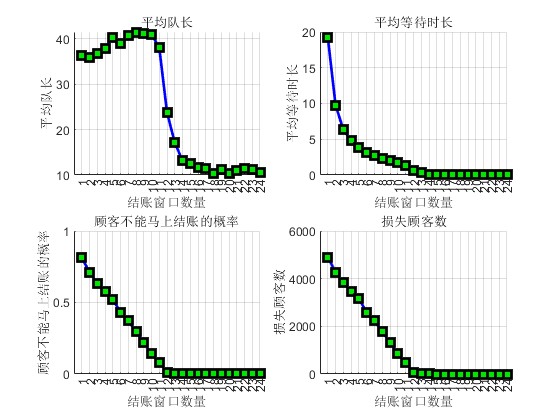
3.算法概述
在人们的日常生活中常常会碰到拥挤和排队现象。去医院看病、在邮局营业窗口等候服务等,这是有形排队。除了有形排队之外,还有无形的排队,比如,由于上网人数多,网速大大减慢,这也是因为在“排队”。
增加资源,如增加服务窗口,多设几条跑道,网站设备扩容等,可以减少顾客排队现象。但当顾客比较少时,必然会造成资源闲置。
由此可见,增加服务机构,当然可以减少排队现象,但却增加了服务成本;反之,减少服务机构,固然提高了服务机构的利用率,降低了成本,但却增加了顾客的排队等待时间。这是相互矛盾的。
我们把顾客和服务方构成的系统称为排队系统。电信网络中的信息流和信道,上网人员和网站设施等,都是顾客和服务员的系统。由于顾客到达和服务时间都是不确定的,绝大多数排队系统工作于随机状态。因此,研究排队系统的复杂性也就在于它的随机性。排队论利用概率论和随机过程理论,研究排队系统内的服务机构和顾客需求之间的关系,以便在所需的服务质量标准得到充分满足的条件下,服务机构的费用最为经济。这就是排队论研究的目的。
4.部分源码
..............................................
%exprnd生成服从指数lamda分布的随机数
arrive_time=exprnd(lamda);
leave_time=[];
current_time=0;
L=0;
LMax=0;
LL=[L];
tt=[current_time];
c=[];
b=[];
e=[];
a_count=0;
b_count=0;
e_count=0;
lamda=1/lamda;
mu=1/mu;
%循环
while min([arrive_time,leave_time])<T
current_time=min([arrive_time,leave_time]);
tt=[tt,current_time]; %记录时间序列
if current_time==arrive_time %顾客到达子过程
arrive_time=arrive_time+exprnd(lamda); %刷新顾客到达事件
a_count=a_count+1; %累加到达顾客数
if L<s %有空闲服务台
L=L+1; %更新队长
if L>LMax
LMax=L;
end
b_count=b_count+1; %累加服务顾客数
c=[c,current_time]; %记录顾客到达时间序列
b=[b,current_time]; %记录服务开始时间序列
leave_time=[leave_time,current_time+exprnd(mu)]; %产生新的顾客离开事件
leave_time=sort(leave_time); %离开事件表排序
elseif L<s+k %有空闲等待位
L=L+1; %更新队长
if L>LMax
LMax=L;
end
b_count=b_count+1; %累加服务顾客数
c=[c,current_time]; %记录顾客到达时间序列
else
e_count=e_count+1; %累加损失顾客数
end
else %顾客离开子过程
leave_time(1)=[]; %从事件表中抹去顾客离开事件
e=[e,current_time]; %记录顾客离开事件序列
if L>s %有顾客等待
L=L-1; %更新队长
if L>LMax
LMax=L;
end
b=[b,current_time]; %记录服务开始时间序列
leave_time=[leave_time,current_time+exprnd(mu)];
leave_time=sort(leave_time); %离开事件表排序
else %无顾客等待
L=L-1; %更新队长
end
end
LL=[LL,L]; %记录队长序列
end
Ws=sum(e-c(1:length(e)))/length(e);
Wq=sum(b-c(1:length(b)))/length(b);
Wb=sum(e-b(1:length(e)))/length(e);
Ls=sum(diff([tt,T]).*LL)/T;
Lq=sum(diff([tt,T]).*max(LL-s,0))/T;
fprintf('到达顾客数:%d\n',a_count); %到达顾客数
fprintf('服务顾客数:%d\n',b_count); %服务顾客数
fprintf('损失顾客数:%d\n',e_count); %损失顾客数
fprintf('平均服务时间:%f\n',Wb); %平均服务时间
fprintf('平均队长:%f\n',Ls); %平均队长
fprintf('平均等待时长:%f\n',Wq); %平均等待时间
if k~=inf
for i=0:LMax
p(i+1)=sum((LL==i).*diff([tt,T]))/T; %队长为i的概率
end
end
P=1-sum(p(1:LMax));
fprintf('顾客不能马上得到服务的概率:%f\n',P); %顾客不能马上得到服务的概率
out=[Ls,Wq,P,e_count];
A375